컴퓨터 공학에서 말하는 그래프(graph)란 이산수학의 그래프 이론의 단방향 그래프(directed graph) 및 무향 그래프(undirected graph)의 개념을 적용하기 위해 가져온 추상적인 데이터 타입이다(출처). 이산수학(discrete mathematics)는 '이산적인' 수학 구조에 대해 연구하는 학문인데, '이산적'과 'discrete'의 사전적 의미는 다음과 같다 (출처).
이산적: 관·명 정보·통신 서로 단절되는. 또는 그런 것. 연속되는 것과 반대되는 것으로 0, 1, 2, 3 따위와 같이 서로 단절되는 값들을 이르는 말이다.
discrete: (같은 종류의 다른 것들과) 별개의 (=seperate)
이산수학은 서로 단절되어 있는, 또는 서로 구분되는 값을 가지는 대상들을 연구하는 학문이다. 이러한 이산수학에서 가져온 개념이기 때문에, 그래프는 비선형적 자료 구조(non-linear data structure)로 구분이 된다. n번째 값 뒤에 n+1이 정해지지 않은 (= 서로 단절되어 있는, 연속하는 것이 아닌) 구조라는 것이다.
아래 이미지와 같이, 그래프는 유한한 정점(vertex)와 간선(edges)의 연결 상태를 보여준다.
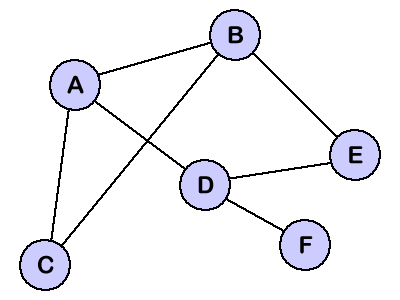
정점(vertex): 여러 개별 자료들. 위 이미지의 알파벳들에 해당된다.
간선(edge): 정점들을 연결하는 선. 방향 및 가중치를 가질 수 있다.
그래프의 간선은 방향을 가지고 있을 수 있다. 아래 예시를 보면, 정점 A에서 B로 가는 간선엔 방향이 표시되어 있다. 이때, B에서 A로는 방향이 없기 때문에 돌아갈 수 없다. 이와 같이 방향이 있는 그래프를 단반향 그래프(directeed graph)라고 한다. 방향이 없는 그래프는 무향 그래프(undireted graph)라고 한다. 무향 그래프의 경우엔 어느 한쪽으로의 이동만 가능하다는 것이 정해져 있지 않으며, 두 정점을 연결하는 간선이 있을 때 양쪽에서 어느 방향으로든 왔다갔다 하는 것이 가능해진다.
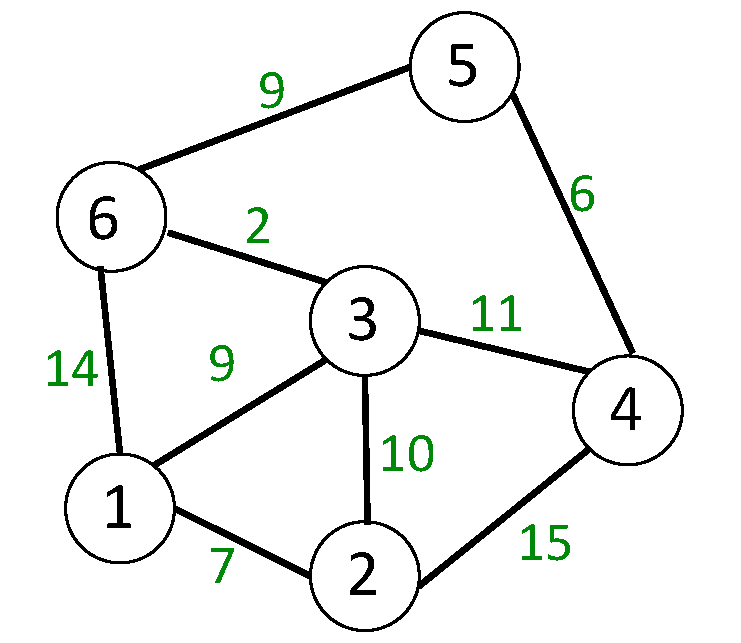
또한, 간선은 가중치를 가질 수 있다. 아래 그래프는 가중치를 가진 간선의 예시이다. 정점 5에서 3으로 가는 길을 찾아본다고 생각해보자. 5에서 3으로 가는 간단한 두 가지 방법은 5 -> 6 -> 3과 5 -> 4 -> 3이 있을 수 있다. 만약 이 그래프의 간선의 가중치가 뜻하는 것이 두 정점 사이의 이동 시간이라면, 어느 길로 가는 것이 더 빠를까? 5에서 6을 거쳐 가는 경로(9+2 = 11)가 5에서 4를 거쳐 가는 경로(6+11 = 17)보다 훨씬 빠를 것이다.
그래프에서 알아두어야할 중요한 개념으로 인접(adjacency)가 있다. 두 정점이 간선으로 이루어진 상태를 보고 인접하다(adjacent)고 한다. 이 인접함의 여부를 가지고 그래프를 코드로 구현할 수가 있는데, 이 때 두 가지 방법이 있다. 인접 행렬(adgancency matrix)과 인접 리스트(adjacency list)가 바로 그 두 가지이다.
1. 인접 행렬 만들기
인접 행렬은 그래프의 정점들감의 인접함을 표시해주는 행렬이다. 다음과 같이 2차원 배열로 작성하게 된다. 다섯개의 정점이 있고, 각 정점들 사이에 간선이 존재하는지 여부를 0 또는 1로 나타낼 수 있다. 아래 예시 코드는 모든 간선 여부를 0 으로 처음 세팅한 모습이다.
let max = 5 // 정점의 갯수
let matrix = new Array(max).fill(0).map((row)=> new Array(max).fill(0))
/*
matrix는 이렇게 생기게 된다:
[
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0]
]
*/
아래는 단방향이면서 가중치가 있는 인접 행렬의 예시이다. 인접행렬의 값이 0이라는건 해당하는 행과 열에 있는 정점들이 서로 연결되지 않았다는 뜻이며, 연결되어 있을 경우엔 각 간선의 가중치가 적혀있다.
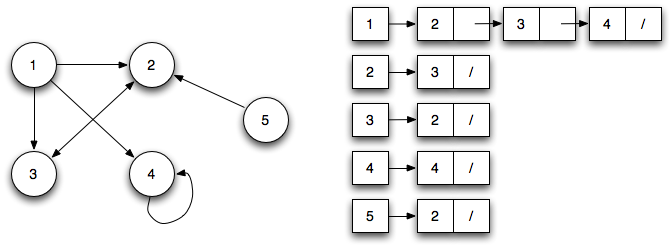
2. 인접 리스트 만들기
인접리스트는 정점들간의 연결 상황을 인접행렬보다 조금 라이트하게 볼 수 있는 표현 방식이다. 인접행렬과 동일한 정보를 알려주지만, 연결 가능한 모든 경우의 수를 저장해서 보여주는 인접행렬과는 다르게 연결되어 있는 경우에만 저장을 하기 때문에 메모리를 조금 덜 사용한다는 장점이 있다.

// 정점의 갯수
let max = 5;
// 인접 리스트를 객체로 만들기 위한 준비!
let adjList = {};
// 정점의 갯수만큼 인접리스트에 키-값을 만든다. 값은 빈 배열로 넣는다.
for (let i = 0; i < max; i++) {
adjLists[i] = []
}
// 정점간 간선 정보에 따라서, loop을 사용해 위에 빈 배열로 만들었던 것에 값을 넣어준다.
// 간선 정보에 따라서, 인접 리스트는 아래와 같은 모양을 하고 있을 것이다.
/*
{
0: [3, 6], // 정점0에서 정점3과 정점6으로 향하는 간선이 있다는 뜻
1: [0],
2: [0, 5],
3: [1, 4],
4: [1, 2],
5: [2, 3, 4]
}
*/
'Learn to Code' 카테고리의 다른 글
| [TIL] node.js 미니 서버 만들기 (0) | 2021.04.30 |
|---|---|
| [TIL] 코드스테이츠 chatterbox (client) 과제 (ongoing) (0) | 2021.04.29 |
| [JS] num++과 ++num의 차이 (0) | 2021.04.10 |
| [JS] 클로저(Closure)란? (0) | 2021.04.10 |
| [JS] 클래스(Class), 인스턴스(Instance), 정적 메소드(Static method), 그리고 서브클래스(Subclassing) (1) | 2021.04.09 |






댓글